Lexikon > Buchstabe C > Carnot-Wirkungsgrad

Carnot-Wirkungsgrad

Der Carnot-Wirkungsgrad (oder Carnot-Faktor), benannt nach dem französischen Physiker Nicolas Léonard Sadi Carnot, ist zunächst der theoretisch mögliche Wirkungsgrad für die Umwandlung von Wärmeenergie in mechanische Energie in einer Wärmekraftmaschine, die auf der Grundlage des sogenannten Carnot-Kreisprozesses (Carnot-Zyklus) arbeitet:

• isotherme Kompression des Arbeitsmediums, wobei Abwärme auf niedrigem Temperaturniveau an ein Kühlmedium abgegeben wird
• weitere Kompression, nun aber ohne Wärmeaustausch (adiabatisch)
• isotherme Expansion, wobei Wärme aus einer Hochtemperatur-Wärmequelle aufgenommen und Arbeit geleistet wird
• weitere adiabatische Expansion (ohne Wärmeaustausch) mit Leisten von Arbeit bis zum Erreichen der ursprünglichen Temperatur

Der Carnot-Wirkungsgrad ist also eine Eigenschaft einer erdachten Maschine in einem stark abstrahierten theoretischen Modell.

Im Rahmen der Theorie der Thermodynamik stellte sich später heraus, dass die genannte Obergrenze für den Wirkungsgrad auch mit keiner anderen Art von Wärmekraftmaschine überschritten werden kann, gleich nach welchem Prinzip sie arbeitet.

Es wird für diese Betrachtung angenommen, dass einer Wärmekraftmaschine eine Wärmequelle (z. B. heißer Dampf) mit einer oberen Temperatur <$T_{o}$> und eine Wärmesenke (z. B. Kühlwasser) mit einer unteren Temperatur <$T_{u}$> zur Verfügung steht. Die Carnot-Formel gibt dann den theoretisch maximal möglichen Wirkungsgrad an zu

$$\eta_\textrm{C} = 1 - \frac{T_\textrm{u}}{T_\textrm{o}}$$ wobei <$T_\textrm{u}$> und <$T_\textrm{o}$> als absolute Temperaturen eingesetzt werden müssen. Die absolute Temperatur ist der Temperaturabstand zum absoluten Nullpunkt, und ihr Wert in der Einheit Kelvin ergibt sich durch das Addieren von 273,15 zur Temperatur in °C. Abbildung 1 zeigt den Carnot-Wirkungsgrad in Abhängigkeit von der oberen Temperatur für zwei verschiedene untere Temperaturen.

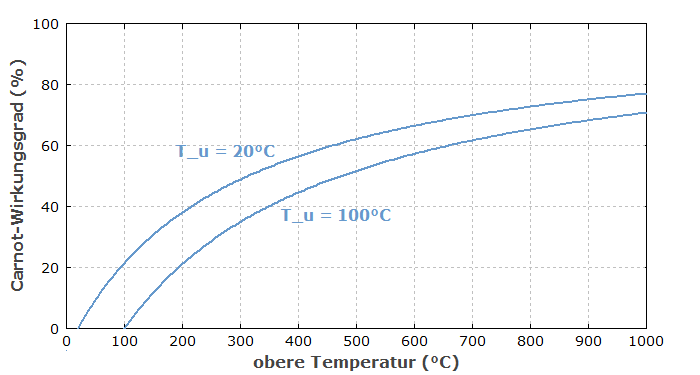
Der Carnot-Wirkungsgrad wird Null, wenn die obere und untere Temperatur gleich sind, also kein Temperaturgefälle zur Verfügung steht. Umgekehrt setzt ein hoher Carnot-Wirkungsgrad ein starkes Temperaturgefälle voraus.

Man beachte, dass sich eine Absenkung der unteren Temperatur um z. B. 1 Grad deutlich stärker auf den Carnot-Wirkungsgrad auswirkt als eine Erhöhung der oberen Temperatur um den gleichen Betrag.

Carnot-Wirkungsgrad und zweiter Hauptsatz der Thermodynamik

Der Physiker Carnot berechnete diesen Wirkungsgrad für einen idealen Kreisprozess, wie er annähernd in manchen Wärmekraftmaschinen (z. B. Dampfturbinen) auftritt. Es stellte sich dann heraus, dass auch jede andere Art von Prozess oder Maschine keinen höheren Wirkungsgrad erreichen könnte, weil dies den zweiten Hauptsatz der Thermodynamik verletzen würde. Im Kern lässt sich das physikalisch so verstehen:

• Die Entnahme von Wärme aus dem oberen Reservoir bewirkt dort eine Reduktion von Entropie.
• Ein Teil dieser Wärme wird in mechanische Energie umgewandelt, die keine Entropie aufweist. Der Anteil dieser Wärme ist der Wirkungsgrad.
• Der nicht umgewandelte Teil der Wärme wird dem unteren Reservoir (z. B. dem Kühlwasser) zugeführt, und dies führt dort zu einer Entropiezunahme. Pro zugeführtem Joule ist diese Entropie höher, weil die Temperatur niedriger ist. (Die Entropiezunahme ist die Wärmemenge dividiert durch die absolute Temperatur.)
• Wenn der Wirkungsgrad höher als der Carnot-Wirkungsgrad wäre, wäre die gesamte Entropieänderung negativ. Genau dies ist jedoch gemäß dem zweiten Hauptsatz der Thermodynamik unmöglich: Die gesamte Entropie eines abgeschlossenen Systems kann nie abnehmen. Eine Maschine, die dies erreichen würde, wird als Perpetuum mobile zweiter Art bezeichnet. Wenn ein solches möglich wäre (was nicht anzunehmen ist), wäre damit der zweite Hauptsatz der Thermodynamik widerlegt (falsifiziert).

Die Berechnung des maximalen Wirkungsgrads auf diese Art ist einerseits viel allgemeiner und andererseits sogar wesentlich einfacher als die für den Carnotschen Kreisprozess, wo die Gasgesetze angewandt werden müssen.

Konsequenzen für die Energietechnik

Um eine maximale Energieeffizienz einer Wärmekraftmaschine zu erreichen, muss erst einmal eine Situation geschaffen werden, in der der Carnot-Wirkungsgrad hoch ist. Hierfür sind zwei Dinge notwendig:

• Die Temperatur der verwendeten Wärmequelle soll möglichst hoch sein. Die wirklich nutzbare Temperatur wird allerdings u. U. durch das begrenzt, was die Maschine aushalten kann. Beispielsweise können die Blätter einer Gasturbine nur mit einer Einlasstemperatur von etwas über 1500 °C arbeiten (bei modernen Großanlagen mit aktiver Kühlung der Blätter). Auch die erhöhte Bildung von Stickoxiden bei hohen Verbrennungstemperaturen kann nachteilig sein.
• Die Temperatur der Wärmesenke soll möglichst tief liegen. Die Kühlung mit Flusswasser ist diesbezüglich günstiger als mit einem Kühlturm; oft wird eine Kombination von Kühlturm und Flusswasserkühlung verwendet, um den Wärmeeintrag in den Fluss zu reduzieren und trotzdem eine sehr niedrige Kondensatortemperatur zu erzielen.

Das Grundprinzip einer Dampfturbinenanlage wird realistischer durch den sogenannten Clausius-Rankine-Kreisprozess beschrieben, der deutlich vom Carnot-Kreisprozess abweicht. Insbesondere erfolgt die Wärmezufuhr nicht auf isotherme Weise. Der für diesen Prozess (wiederum mit gewissen Idealisierungen) errechnete Wirkungsgrad liegt deutlich tiefer als der Carnot-Wirkungsgrad, und tatsächlich realisierte Maschinen auf der Basis dieses Prinzips sind wiederum etwas weniger effizient.

Bei modernen Gasturbinen und Dampfturbinen kann der Carnot-Wirkungsgrad aber immerhin einigermaßen angenähert werden. Hierzu dienen insbesondere auch als Carnotisierung bezeichnete Maßnahmen, die den verwendeten Prozess dem Carnot-Prozess stärker annähern. Bei den modernsten Gas-und-Dampf-Kombikraftwerken wird ein Wirkungsgrad von immerhin ca. 60 % erreicht, während der Carnot-Wirkungsgrad für 1500 °C Einlass der Gasturbine und 45 °C unterer Temperatur der Dampfturbine 82 % betragen würde.

Wenn die Abwärme genutzt werden soll (→ Kraft-Wärme-Kopplung), ist dafür häufig eine gewisse Anhebung der unteren Temperatur notwendig, was den Carnot-Wirkungsgrad reduziert. Man erhält dann eine etwas reduzierte Ausbeute an mechanischer bzw. elektrischer Energie, dafür aber einen höheren Gesamtwirkungsgrad. Man beachte aber, dass die Anhebung der Kühltemperatur um ein Kelvin den Carnot-Wirkungsgrad deutlich stärker verringert als die Absenkung der oberen Temperatur um ein Kelvin.

"Offene" Systeme wie Ottomotoren und Dieselmotoren arbeiten nach Funktionsprinzipien, die weit vom Carnot-Prozess abweichen. Trotzdem kann der Carnot-Wirkungsgrad aus der Verbrennungstemperatur und der Temperatur der eingelassenen Luft berechnet werden, um eine obere Grenze für den möglichen Wirkungsgrad zu erhalten. In der Praxis erzielbare Werte liegen jedoch erheblich darunter.

Geothermische Kraftwerke müssen meist mit einem recht niedrigen oberen Temperaturniveau arbeiten und können deswegen keinen hohen elektrischen Wirkungsgrad erzielen.

Siehe auch: Wirkungsgrad, Wärmekraftmaschine, Energieeffizienz, Temperatur, Entropie, Thermodynamik, Hauptsätze der Thermodynamik, thermodynamisch optimiertes Heizen