Lexikon > Buchstabe C > Clausius-Rankine-Kreisprozess

Clausius-Rankine-Kreisprozess

Der Clausius-Rankine-Kreisprozess ist ein vereinfachtes thermodynamisches Modell für geschlossene Kreisprozesse, wie sie in Dampfturbinen und Dampfmaschinen technisch realisiert werden. Es wurde benannt nach dem deutschen Physiker Rudolf Julius Emanuel Clausius und dem schottischen Ingenieur William John Macquorn Rankine und spielte eine wesentliche Rolle bei der Bemühung, die thermodynamischen Grundlagen und die prinzipiellen Begrenzungen des Wirkungsgrads von Dampfturbinen zu verstehen.

Allgemein spricht man von einem thermodynamischen Kreisprozess, wenn ein Arbeitsmedium wie beispielsweise Wasser in einer Maschine oder Anlage eine Reihe von Zustandsänderungen (beispielsweise Änderungen von Temperatur, Druck und Aggregatszustand) durchläuft, die sich periodisch (also immer gleich) wiederholen. Man betrachtet dabei also eine Maschine oder Anlage, die im stationären Zustand arbeitet, d. h. sich unter konstanten äußeren Bedingungen in etlichen Zyklen auf diese eingestellt hat. Ein geschlossener Kreisprozess liegt vor, wenn es im Betrieb keinen stofflichen Austausch des Arbeitsmediums mit der Umgebung gibt. Dies ist bei Dampfturbinenanlagen in der Regel der Fall, zum Teil auch bei Dampfmaschinen, in der Regel nicht aber bei Gasturbinen.

Grundlegend geht es beim Clausius-Rankine-Kreisprozess um die Realisierung einer Wärmekraftmaschine, die also Wärme zum Teil in mechanische Energie umwandelt. Zum fundamentalen Prinzip gehört, dass das Arbeitsmedium abwechselnd komprimiert und expandiert wird, wobei die Bedingungen so eingestellt werden, dass man zur Kompression weniger mechanische Arbeit leisten muss, als das Medium bei der Expansion leistet. Dies bedeutet, dass in einem gesamten Zyklus der Maschine mechanische Energie übrig bleibt, die als Nutzenergie entnommen werden kann. Beim Clausius-Rankine-Kreisprozess verwendet man ein Arbeitsmedium wie Wasser, welches beim Prozess abwechselnd in flüssiger und gasförmiger Phase vorhanden ist.

Die vier Schritte des Clausius-Rankine-Kreisprozesses

Der Clausius-Rankine-Kreisprozess kann folgendermaßen beschrieben werden:

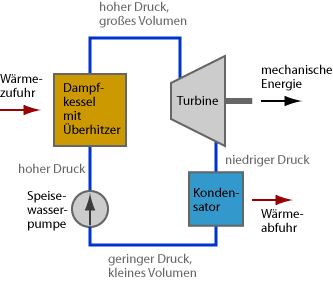
• Das zunächst flüssige Arbeitsmedium wird bei konstantem hohem Druck stark erwärmt und dabei verdampft, wobei die Entropie des Mediums stark zunimmt. Hier treten eigentlich drei Prozesse auf: zunächst die Erwärmung bis zum Siedepunkt, dann das Verdampfen (was den größten Teil der Wärmezufuhr benötigt) und schließlich eine weitere Erhitzung (Überhitzung) des Dampfs. (Hierbei wird angenommen, dass der Druck unterhalb des kritischen Drucks bleibt, sodass es eine klare Unterscheidung zwischen flüssiger und gasförmiger Phase gibt.) In der Praxis kann dies beispielsweise in einem Dampfkessel geschehen, dem Wärme zugeführt wird, die aus der Verbrennung eines Brennstoffs oder in einem Kernreaktor gewonnen wird.
• Das Arbeitsmedium wird nun expandiert, ohne weiter Wärme mit seiner Umgebung austauschen zu können (adiabatische Expansion). Dabei leistet es Arbeit, d. h. es gibt mechanische Energie ab, und seine Temperatur sinkt dabei stark ab, wobei die Entropie im Idealfall unverändert bleibt. Der Dampf kann bei der Expansion teilweise kondensiert werden. Dieser Schritt kann beispielsweise in einer oder mehreren Turbinen oder Hubkolbenmaschinen erfolgen.
• Anschließend wird der restliche Dampf kondensiert, indem man ihm bei niedriger Temperatur Wärme entzieht. Im verwendeten Modell wird angenommen, dass der Druck hierbei konstant bleibt, nämlich auf dem Niveau, das am Ende der Expansionsphase erreicht wird. Die Temperatur bleibt im Nassdampfgebiet ebenfalls konstant, und die Entropie des Mediums sinkt stark ab. In der Praxis verwendet man für diesen Schritt einen sogenannten Kondensator, der beispielsweise ein mit kaltem Wasser gekühlter Wärmeübertrager sein kann.
• Um wieder zum ursprünglichen Zustand zurückzukehren, muss das flüssige Medium nun mit einer Pumpe wieder auf den ursprünglichen hohen Druck gebracht werden (wiederum ohne Wärmeaustausch mit der Umgebung), mit dem es in den Dampferzeuger geleitet werden kann. Die Pumpe muss hierbei Arbeit verrichten – allerdings sehr viel weniger, als das Medium bei der Expansion geleistet hat, weil das zu fördernde Volumen in flüssiger Form weitaus geringer ist. Die Pumpe verbraucht also nur einen kleinen Teil der freigesetzten mechanischen Energie.

Analyse des Kreisprozesses; erreichbarer Wirkungsgrad

Der Prozess kann nun quantitativ analysiert werden, wobei die physikalischen Eigenschaften des Arbeitsmediums (Zustandsgleichungen und Verdampfungs- bzw. Kondensationsenthalpie) zu berücksichtigen sind. Aus den Resultaten kann der Wirkungsgrad der mit diesem Kreisprozess arbeitenden Maschine abgeschätzt werden, wobei allerdings wegen diverser Vereinfachungen (Idealisierungen) Abweichungen auftreten; eine reale Maschine ist etwas weniger effizient als Folge zusätzlicher Strömungsdruckverluste (Reibungsverluste), Undichtigkeiten, unerwünschter Wärmeleitung usw., die im theoretischen Modell nicht berücksichtigt werden.

Der berechnete Wirkungsgrad ist umso höher, je höher die Temperatur des erzeugten Dampfs ist und je stärker das Medium expandiert werden kann. Die mögliche Stärke der Expansion wird umso größer, je niedriger die Temperatur ist, bei der die Abwärme abgeführt werden kann. Der Wirkungsgrad kann den sogenannten Carnot-Wirkungsgrad prinzipiell nicht übertreffen und bleibt in der Tat sogar deutlich unter diesem; beispielsweise berechnet man für eine Dampftemperatur von 400 °C und die Kondensation bei 25 °C einen Wirkungsgrad von 39,5 %, während der Carnot-Wirkungsgrad 55,7 % wäre.

Der geringere Wirkungsgrad rührt daher, dass der Clausius-Rankine-Kreisprozess thermodynamisch nicht optimal ist. Insbesondere ist es nicht optimal, für die Erwärmung des Arbeitsmediums ausschließlich die von außen zugeführte Wärme zu verwenden. Es wäre effizienter, für die Erwärmung auf niedrigem Temperaturniveau zunächst Entnahmedampf aus der Turbine einzusetzen, was in heutigen Kraftwerken auch so praktiziert wird. Ebenfalls ist heute eine sogenannte Zwischenüberhitzung des Dampfs zwischen den Turbinenstufen üblich, was ebenfalls den Wirkungsgrad verbessert und außerdem die letzte Turbinenstufe schont. Solche Maßnahmen werden als Carnotisierung bezeichnet, weil sie den Wirkungsgrad dem idealen Carnot-Wirkungsgrad näher bringen.

In den allermeisten Fällen wird Wasser als Arbeitsmedium verwendet – beispielsweise in fast allen Dampfturbinen-Kraftwerken. Wenn allerdings nur eine Wärmequelle mit relativ niedriger Temperatur zur Verfügung steht, sind die thermodynamischen Eigenschaften von Wasser nicht optimal oder machen dieses sogar völlig ungeeignet. In solchen Fällen setzt man manchmal organische Arbeitsmedien mit wesentlich niedrigerem Siedepunkt ein und spricht bei diesem modifizierten Verfahren dann vom Organic Rankine Cycle.

Siehe auch: Thermodynamik, Dampfturbine, Dampfmaschine, Wirkungsgrad