Exponentielles Wachstum – für Laien verständlich erklärt
Autor: Dr. Rüdiger Paschotta

Der Begriff des exponentiellen Wachstums begegnet einem in verschiedensten Zusammenhängen – aktuell in Diskussionen der von Coronaviren ausgelösten Covid-19-Pandemie. Hierbei scheitern Einschätzungen oft daran, dass die Charakteristika exponentiellen Wachstums nicht vollständig verstanden wurden. Dieses Problem tritt auch in anderen Zusammenhängen immer wieder auf. Hier soll deswegen versucht werden, diese Sache auch für Laien verständlich umfassend aufzuklären. Es geht um die folgenden zentralen Fragen:
- Was genau bedeutet exponentielles Wachstum?
- Was sind seine besonderen Eigenschaften?
- Wann tritt exponentielles Wachstum auf, und warum beobachtet man es so häufig?
- Wie kann man diese Art von Wachstum grafisch darstellen?
- Kann exponentielles Wachstum unbegrenzt fortschreiten?
- Wie kann man einen exponentiellen Abfall verstehen, und wo kommt er vor?
Hierbei soll nur ein absolutes Minimum an mathematischen Formeln verwendet werden. Sollte es Ihnen auch hierfür am nötigen Grundlagenwissen fehlen, dürfte trotzdem der Großteil des Artikels verständlich bleiben; lediglich können Sie einige Feststellungen dann eben nicht selbst nachprüfen.
Wir werden die Grundprinzipien anhand einer Reihe interessanter Beispiele diskutieren – in unterschiedlichsten Themenbereichen wie Bakterienwachstum, Epidemien, Kapitalanlage, virale Nachrichten, Atombomben, Kernreaktoren, Lasertechnik und Oszillatoren. So sollte das eine ziemlich lehrreiche Sache werden.
Was genau ist exponentielles Wachstum?
Einfache Antwort auf eine einfache Frage: Das ist ein Wachstum, welches durch eine sogenannte Exponentialfunktion beschrieben werden kann. Beispielsweise kann die zeitliche Entwicklung einer Größe ($A$) – etwa der Anzahl Bakterien in einer Nährlösung – bei exponentiellem Wachstum durch die folgende Formel mit der natürlichen Exponentialfunktion beschrieben werden:
$$A(t) = A_0 \, e^{\alpha t}$$
wobei das oft auch als ($A(t) = A_0 \cdot \exp(\alpha t)$) geschrieben wird. Hier steht ($t$) für die Zeit (engl. time), und ($A(t)$) bedeutet den Wert von ($A$) zur Zeit ($t$). Zur Zeit ($t = 0$), was oft für den Beginn der Betrachtung gewählt wird, erhalten wir den Anfangswert: ($A(0) = A_0$), weil eine Exponentialfunktion angewandt auf den Wert null immer 1 ergibt. (Ausnahme: 00 ist undefiniert.) Das Symbol ($e$) steht für die sogenannte Eulersche Zahl und ist ungefähr 2,71828. (Andere Exponentialfunktionen verwenden eine andere "Basis" als ($e$), z. B. oft 2 oder 10.) Außerdem ist ($\alpha$) eine Konstante, d. h. ein nicht zeitlich veränderlicher Wert; man bezeichnet sie oft als Wachstumskoeffizient.
Natürlich wächst die betrachtete Größe ($A(t)$) umso schneller an, je größer ($\alpha$) ist. Mit einem Taschenrechner können Sie ($e^{\alpha t}$) für irgendwelche Werte von ($\alpha$) und ($t$) leicht ausrechnen; die Taste für die Anwendung der Exponentialfunktion ist meist mit EXP beschriftet.
Potenzen mit ganzzahligem Exponenten begegnet man in der Schule schon relativ früh. So ist beispielweise ($\exp(5) = e^5 = e \cdot e \cdot e \cdot e \cdot e$) (5 Faktoren ($e$)). Wie man das für eine "krumme" Zahl von Faktoren wie z. B. 2,478 durchführen sollte, bleibt damit zunächst ein Rätsel. Sie ahnen schon: Es muss eine ganz andere Methode geben, die Exponentialfunktion auszuwerten, die für beliebige, also nicht nur für ganzzahlige Werte funktioniert; diese Diskussion würde hier aber zu weit gehen.
Nicht verwechseln sollten Sie Exponentialfunktionen mit Potenzfunktionen. Der Unterschied ist, dass wir bei einer Exponentialfunktion eine feste Basis haben (z. B. ($e$) oder 10), während der Exponent variabel ist; bei Potenzfunktionen ist es umgekehrt. Übrigens steigt eine Exponentialfunktion auf Dauer schneller an als jede Potenzfunktion, egal wie hoch deren Exponent ist.
Das alles ist zunächst einmal eine mathematische Sache. Was soweit noch nicht erklärt wurde: Warum kommt so etwas in der Realität häufig vor, bzw. unter welchen Umständen? Bevor wir uns damit beschäftigen, sollten wir aber eine wichtige Eigenschaft der Exponentialfunktion etwas studieren:
Die Wachstumsgeschwindigkeit
Zuerst möchte ich erklären, was man unter einer Wachstumsgeschwindigkeit versteht: Es ist die Zunahme (oder allgemeiner Veränderung) der jeweiligen Größe pro Zeiteinheit. Rechnerisch: die Änderung der Größe (bezeichnet als ($d A$)) dividiert durch die Länge des Zeitintervalls: ($d A/d t$).
Im Beispiel des Bakterienwachstums, wo die interessierende Größe ($A$) die momentane Zahl der Bakterien ist, ist die Wachstumsgeschwindigkeit (formelmäßig bezeichnet als ($d A/d t$) oder auch ($A'(t)$)) die Zunahme dieser Anzahl pro Sekunde, Stunde oder Tag – je nachdem welche Zeiteinheit wir dafür verwenden.
Wenn die Wachstumsgeschwindigkeit konstant ist, nimmt die Größe gleichmäßig (linear zu), aber im Allgemeinen verändert sich die Wachstumsgeschwindigkeit mit der Zeit.
Ein mathematisches Detail: So weit wäre die Wachstumsgeschwindigkeit nicht für einen bestimmten Zeitpunkt definiert, sondern für ein mehr oder weniger großes Zeitintervall (z. B. eine Stunde). Mathematisch kann man aber die Wachstumsgeschwindigkeit für einen bestimmten Augenblick ermitteln, indem man den sogenannten Grenzwert für immer kürzer werdende Zeitintervalle ermittelt. Diesen Grenzwert bezeichnet man als zeitliche Ableitung – ein zentrales Konzept der sogenannten Differentialrechnung. Streng genommen funktioniert diese Grenzwertbildung genau für das Beispiel der Bakterien nicht, da es keine beliebig kleine Änderung der Bakterienzahl geben kann, aber solche Details sind für die folgenden Betrachtungen nicht von zentraler Bedeutung.
In manchen Fällen ist die Wachstumsgeschwindigkeit proportional zum bereits vorhandenen Wert von ($A$), das heißt sie ist zu jedem Zeitpunkt dieser Wert multipliziert mit einem konstanten Wert($\alpha$):
$$\frac{\partial A(t)}{\partial t} = A_0 \, \alpha \, e^{\alpha t} = \alpha \, A(t)$$
Definitionsgemäß spricht man genau in solchen Fällen von einem exponentiellen Wachstum. Hier verdoppelt sich die Wachstumsgeschwindigkeit beispielsweise, wenn ($A$) doppelt so groß geworden ist, was ein immer weiter beschleunigtes Wachstum bedeutet. Umgekehrt gilt natürlich auch: Wenn das Wachstum exponentiell ist, ist die Wachstumsgeschwindigkeit proportional zum Wert der wachsenden Größe selbst.
Wir werden im Folgenden sehen, dass solche Fälle ziemlich häufig auftreten.
Wann tritt exponentielles Wachstum auf?
Die oben genannte einfache Bedingung für exponentielles Wachstum ist in der Realität ziemlich häufig erfüllt, zumindest näherungsweise. Zwei Beispiele hierfür:
- Wenn sich die Anzahl von Bakterien in einer Nährlösung verzehnfacht hat, verzehnfacht sich auch die Anzahl der pro Sekunde neu durch Zellteilung gebildeten Bakterien – einfach weil sich nun ja zehnmal mehr Bakterien teilen können. (Das muss freilich nicht immer so sein; wir werden das später diskutieren.)
- Wenn Ihr Guthaben auf einem Sparkonto auf das Doppelte angewachsen ist, bekommen Sie jedes Jahr auch doppelt so viel Zinsen, die Sie wieder anlegen können.
Es ist eben oft so, dass das Wachstum genau von dem bestimmt wird, was schon da ist, und genau deswegen treffen wir exponentielles Wachstum in der Realität so oft an, zumindest näherungsweise.
In Physik und Technik wird die zeitliche Entwicklung einer Größe häufig durch eine Differentialgleichung beschrieben – also durch eine Gleichung, die einen Zusammenhang zwischen einer Größe, ihrer Ableitung und ggf. noch anderen Dingen herstellt. Wenn sie die genannte einfache Form hat – eine Ableitung proportional zum momentanen Wert der Größe – erkennt man dies sofort und kann eine Exponentialfunktion als Lösung angeben. Lösung bedeutet hier eine Funktion, die die Differentialgleichung erfüllt und ggf. noch zusätzliche Bedingungen. Natürlich gibt es auch viele andere Differentialgleichungen, die auch andere Lösungen haben.
Beispiel: Bakterien in einer Nährlösung
Nehmen wir an, dass wir anfangs (d. h. zur Zeit ($t = 0$)) 1000 Bakterien in einer Nährlösung in einem Reagenzglas haben (also ($A_0$) = 1000) und dass ($\alpha$) = 1 /h (1 pro Stunde) ist – ein für viele Bakterien realistischer Wert. In diesem Fall nimmt die Zahl Bakterien in jeder Stunde um den Faktor ($e$) ≈ 2,71828 zu. Die folgende Tabelle zeigt die zeitliche Entwicklung über einige Stunden:
| Zeit | 0 h | 1 h | 2 h | 3 h | 4 h | 5 h |
|---|---|---|---|---|---|---|
| Anzahl | 1000 | 2 718 | 7 389 | 20 086 | 54 598 | 148 413 |
Das könnten Sie mit einem Taschenrechner leicht nachprüfen. Natürlich wurden die Zahlen jeweils auf ganze Werte gerundet.
Betrachten wir die Entwicklung einmal über einen etwas größeren Zeitraum, nämlich über fünf Tage:
| Zeit | 0 Tage | 1 Tage | 2 Tage | 3 Tage | 4 Tage | 5 Tage |
|---|---|---|---|---|---|---|
| Anzahl | 1000 | 26,5 · 1012 | 7,02 · 1023 | 1,86 · 1034 | 4,92 · 1044 | 1,3 · 1055 |
Wir haben also beispielsweise nach einem Tag schon 26,5 · 1012 Bakterien. Hier musste ich die Resultate mit Zehnerpotenzen darstellen, da die Darstellung sonst zu lange würde; beispielsweise ist 1012 = 1 000 000 000 000, also eine 1 mit 12 Nullen dahinter (eine Billion).
Sie sehen, dass die Zahl innerhalb weniger Tage exorbitant ansteigt. Ohne Verwendung von Zehnerpotenzen würde die Länge der Zahlendarstellung etwa linear anwachsen; mit Zehnerpotenzen sehen Sie dasselbe am Exponenten. Wenn man mit exponentiellem Wachstum nicht vertraut ist, unterschätzt man das langfristige Wachstum in der Regel ganz massiv. Sicherlich hätten viele Leser nach Betrachtung der ersten Tabelle – mit der Entwicklung über einige Stunden – gedacht, dass es im Laufe einiger Tage einige Millionen oder Milliarden werden, und nicht etwa viele Trillionen nach bereits einem Tag und noch weit, weit mehr nach wenigen Tagen. Wer etwas Erfahrung damit hat, wird zumindest das gefühlsmäßige Schätzen unterlassen und stattdessen lieber ein wenig rechnen.
In der Praxis ist ein so dramatisches Wachstum auf Dauer natürlich nicht möglich, alleine weil so viele Bakterien schon längst nicht mehr in ein Reagenzglas passen würden. Wenn beispielsweise jedes Bakterium eine Masse von einem Pikogramm (1 pg) hat – das ist ein Billionstel Gramm –, dann hätten eine Trillion Bakterien (erreicht nach ca. 34,5 Stunden) zusammen bereits eine Masse von einer Tonne; dafür bräuchte man ein ungewöhnlich großes Reagenzglas. Deswegen ist ein realistisches Szenario, dass das Wachstum anfangs zwar durchaus exponentiell ist, dann aber irgendwann mehr oder weniger drastisch abnimmt. Wir werden uns weiter unten noch mit den Grenzen des Wachstums beschäftigen.
Die (hypothetische) exponentielle Entwicklung kann man auch mit einem Diagramm darstellen, hier für die ersten 36 Stunden:
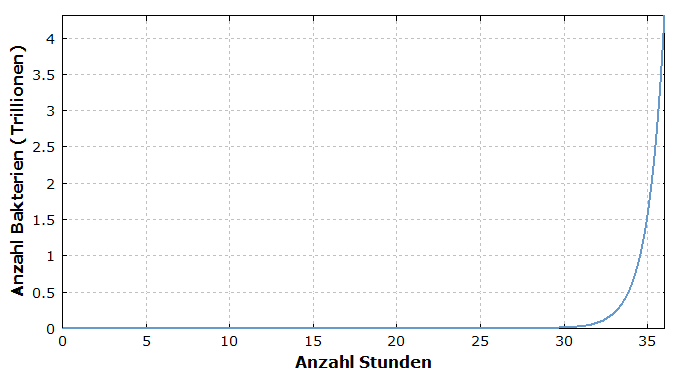
Sie sehen, dass sich in den ersten 30 Stunden so gut wie nichts zu tun scheint: Die blaue Kurve bleibt sehr nahe an der y-Achse (der unteren Linie). Danach geht plötzlich die Post ab: Es sieht so aus, als würde das Wachstum erst hier plötzlich loslegen. In Wirklichkeit aber ist aber das relative Wachstum die ganze Zeit lang konstant: Jede Bakterie verhielt sich von Anfang an gleich wie später, und in jeder einzelnen Stunde steigt die Anzahl der Bakterien um den gleichen Faktor (hier ca. 2,718). Wenn übrigens der Wachstumskoeffizient nur halb so groß gewesen wäre (0,5 /h), müssten wir einfach doppelt so lange warten, um das gleiche Wachstum zu erhalten.
Wenn man das Diagramm mit einer logarithmischen y-Achse zeichnet, kann man das Wachstum von Anfang an genau verfolgen:
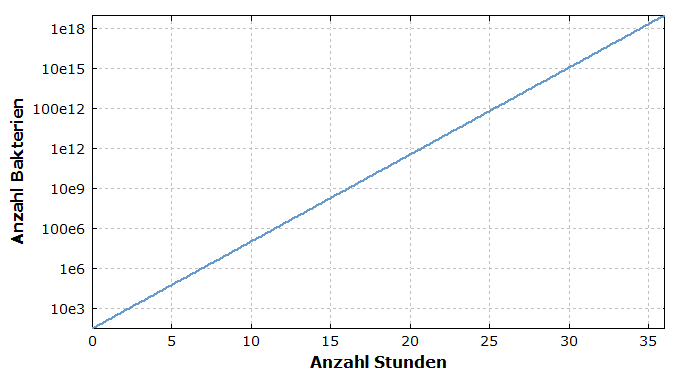
Beachten Sie, dass sich hier die Zahl der Bakterien immer um den Faktor 100 erhöht, wenn man von einer gestrichelten horizontalen Linie zur nächsten kommt. Dies geschieht in unserem Beispiel innerhalb von ca. 4,6 Stunden.
In einem solchen halb-logarithmischen Diagramm (mit logarithmischer Skalierung nur für die vertikale, nicht aber die horizontale Achse) sieht man ein exponentielles Wachstum immer als eine gerade Linie – das ist eine grundlegende Eigenschaft der Exponentialfunktion. Weil dieser lineare Verlauf ziemlich nützlich ist, verwendet man diese Art von Darstellung in der Wissenschaft häufig. Man kann damit das weitere Wachstum auch leicht grafisch extrapolieren (in die Zukunft fortschreiten) unter der Annahme, dass es weiterhin exponentiell erfolgen wird: Man verlängert einfach die bisher beobachtete Gerade nach rechts. Natürlich kann es sein, dass das exponentielle Wachstum irgendwann gestoppt wird, die Extrapolation also schief läuft – zu den Gründen dafür später mehr.
Diverse Fragen
Bestimmte Fragen tauchen hier häufig auf:
Ist exponentielles Wachstum rasend schnell?
Manchmal wird behauptet, exponentielles Wachstum sei immer rasend schnell. Das würde ich so nicht sagen: Anfangs ist es ja durchaus langsam. Genau deswegen wird es ja anfangs oft sehr unterschätzt. Nur nimmt die Wachstumsgeschwindigkeit dann eben ständig zu und wird irgendwann riesig groß.
Natürlich spielt auch die Größe des Wachstumskoeffizienten (in den obigen Formeln der Wert von ($\alpha$)) eine Rolle. Beispielsweise ist dieser beim Wachstum der Weltbevölkerung relativ gering, sodass nur über ganze Generationen hinweg eine erhebliche Zunahme zu sehen ist – was natürlich trotzdem eine Reihe ernster Probleme verursacht.
Warum sehen die Wachstumskurven so unterschiedlich aus?
Wie oben gezeigt, erhält man für ein halb-logarithmisches (semilogarithmisches) Diagramm bei exponentiellem Wachstum immer eine Gerade. Mit linearer Skalierung der Achsen dagegen ist es eine immer schneller anwachsende Kurve, die man aber mit recht unterschiedlichen Formen vorfindet. Betrachten Sie beispielsweise die beiden folgenden Diagramme für das Bakterienwachstum:
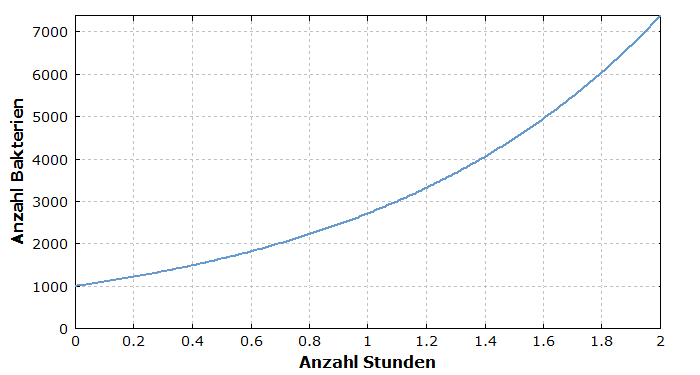

Nur im zweiten Diagramm haben wir den Eindruck, dass lange praktisch nichts geschieht und es dann plötzlich voll losgeht. Der Unterschied ist einfach der, dass im ersten Diagramm nur die Entwicklung über einen kurzen Zeitraum dargestellt wird, innerhalb dessen die wachsende Größe nur um einen Faktor von hier ca. 7 ansteigt. Mit dem wesentlich längeren Zeitraum im zweiten Diagramm ist die Zunahme weitaus größer, wodurch diese spezielle Charakteristik der Kurve entsteht. Man sieht am Anfang noch überhaupt kein Ansteigen, weil die relativ geringen Werte auf einer Skala, die die Darstellung des Endresultats noch zulässt, verschwindend gering erscheinen.
So manche Täuschung – etwa in den Anfangszeiten in der Coronaviren-Krise zu beobachten, erschreckenderweise teils sogar bei Virologen – rührt im Kern daher, dass man für einige Zeit nur sehr geringe Werte wahrnimmt, deren exponentielles Wachstum nicht beachtet (obwohl man es z. B. bei sinnvoller grafischer Darstellung sofort erkennen könnte) und sich deswegen sicher fühlt. Irgendwann kommt dann eben die böse Überraschung.
Warum begegnet man hier öfters Logarithmen?
Sie haben oben gesehen, dass man häufig halb-logarithmische Diagramme zur Darstellung exponentiellen Wachstums verwendet, und auch sonst (z. B. im Zusammenhang mit der Halbwertszeit, siehe unten) begegnen einem Logarithmen in diesem Zusammenhang relativ häufig. Dies liegt einfach daran, dass beispielsweise der natürliche Logarithmus die mathematische Umkehrung der natürlichen Exponentialfunktion ist. Analog ist der Zehnerlogarithmus die Umkehrung der Exponentialfunktion mit Basis 10.
Ein Beispiel hierfür: Wenn bei der oben beschriebenen Exponentialfunktion die Zeit so weit voranschreitet, dass ($\alpha \: t$) um 17 größer wird, steigt die Funktion um den Faktor exp(17) ≈ 24,1 Millionen an. Umgekehrt ergibt der natürliche Logarithmus von 24,1 Millionen wieder ca. 17. Beim Taschenrechner finden Sie dafür meist eine mit "ln" beschriftete Taste – manchmal auch "log", was aber weniger klar ist; es könnte dann beispielsweise auch der Zehnerlogarithmus sein, den man besser mit "lg" bezeichnet, um Verwechslungen zu vermeiden.
Kann exponentielles Wachstum unbegrenzt fortschreiten?
Mathematisch gesehen ja, in der Realität aber nicht. Dort stößt ein exponentielles Wachstum früher oder später an Grenzen. Was genau passiert dann?
Betrachten wir das Beispiel der Bakterienkultur. Sie leben von einer Nährlösung und verbrauchen diese mehr und mehr. Selbst wenn man die Nährstoffe irgendwie ständig ersetzen und die Ausscheidungsprodukte abführen würde, gelänge es früher oder später nicht mehr, die Nährlösung in einem solchen Zustand zu halten, dass die Bakterien weiter prächtig wachsen können. Sie stoßen also unweigerlich an Grenzen dadurch, dass ihre Lebensgrundlagen aufgebraucht werden. Es ist ja auch klar, dass dieses Wachstum aufhören muss, deutlich bevor die Bakterien die gesamte Masse der Erde hätten – und dies wäre ja in unserem Beispiel bei unbegrenztem Wachstum ziemlich schnell erreicht, nämlich innerhalb von gut dreieinhalb Tagen.
Ähnlich passiert es in vielen anderen Zusammenhängen auch. Wenn irgendeine Größe durch starkes Wachstum ein genügend großes Maß erreicht hat, beginnt sie Auswirkungen zu haben, die häufig das weitere Wachstum ausbremsen.
Mathematisch drückt sich das dadurch aus, dass der Wachstumskoeffizient nicht mehr konstant bleibt, sondern irgendwann absinkt.
Exponentieller Abfall
Exponentiell kann nicht nur ein Wachstum erfolgen, sondern auch ein Abfallen (eine Abnahme). Mathematisch erhält man dies, wenn der Wachstumskoeffizient negativ wird. Bei Exponentialfunktionen gilt die Regel, dass man den Kehrwert des ursprünglichen Resultats erhält, wenn man den Exponenten vom Positiven ins Negative wendet.
Beispiel: ($e^5$) ≈ 148.4, ($e^{-5}$) ≈ 1 / 148.4 ≈ 0.00674.
Betrachten wir als physikalisches Beispiel den radioaktiven Zerfall von Cäsium 137, einem der Spaltprodukte des Urans, das in radioaktiven Abfällen vorkommt. Wir starten also mit einer bestimmten Menge davon und sehen, wie sich diese mit der Zeit dadurch verringert, dass sich diese instabilen Atome unter Aussendung radioaktiver Strahlung in andere Arten von Atomen umwandeln. Für das einzelne Atom ist dies ein zufälliger (also nicht vorhersagbarer) Prozess, aber für eine große Anzahl von Atomen kann man sehr gut mit Durchschnittswerten rechnen. Wichtig ist die Feststellung, dass die Anzahl der pro Sekunde zerfallenden Cäsium-Atome proportional ist zu deren Anzahl. Klar: Je mehr man von diesen Atomen hat, desto mehr von ihnen zerfallen pro Sekunde. Dadurch haben wir eine negative Wachstumsgeschwindigkeit ihrer Anzahl, die proportional zu dieser Anzahl selbst ist. Dies führt mathematisch wieder zu einer Exponentialfunktion, nur diesmal eben mit einem negativen Koeffizienten.
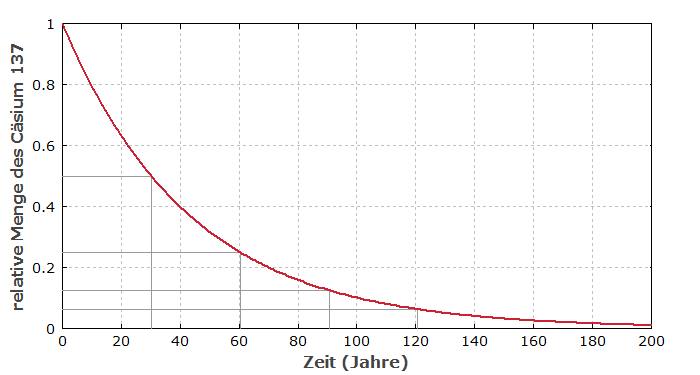
Bei exponentiellem Abfall gibt man häufig die sogenannte Halbwertszeit ($T_{1/2}$) an – das ist die Zeit, nach der noch die Hälfte der ursprünglichen Menge da ist. Sie lässt sich ganz einfach aus dem genannten Koeffizienten berechnen:
$$T_{1/2} = \frac{ln 2}{|\alpha|}$$
Hierbei ist ($\ln 2$) ≈ 0.693, der natürliche Logarithmus von 2.
Bei exponentiellem Wachstum kann man ganz analog eine Verdoppelungszeit berechnen.
Natürlich kommt es in der Realität (z. B. auch in Physik und Technik) wiederum sehr häufig vor, dass eine negative Wachstumsgeschwindigkeit betragsmäßig proportional zum momentanen Wert einer abfallenden Größe ist. Immer dann kommt es zu einem exponentiellen Abfall.
Auch exponentieller Abfall kommt natürlich mit ganz unterschiedlichen Geschwindigkeiten vor. Beispielsweise bei der Radioaktivität: Während die Halbwertszeit mancher radioaktive Nuklide ein winziger Bruchteil einer Sekunde ist, beträgt sie bei anderen Nukliden viele Milliarden von Jahren.
Weitere Beispiele für exponentielles Wachstum oder Abfallen
Im Folgenden betrachten wir noch ein paar weitere Beispiele und deren besondere Umstände sowie relativ leicht nachvollziehbare Schlussfolgerungen.
Epidemien
Eine Epidemie, die durch Infektionen mit Bakterien oder Viren verursacht wird, breitet sich durch die Übertragung dieser Krankheitserreger zwischen Menschen aus. Ein solcher Übertragungsvorgang wird natürlich in einer Bevölkerung umso wahrscheinlicher, je mehr Menschen bereits infiziert sind. Solange die Wahrscheinlichkeit, dass ein Infizierter jemand anderes ansteckt konstant und hoch genug bleibt, kommt es zu einem exponentiellen Wachstum.
Häufig betrachtet man den sogenannten Reproduktionsfaktor – die durchschnittliche Anzahl derjenigen, die durch einen Infizierten angesteckt werden. Ein exponentielles Wachstum ergibt sich, wenn der Reproduktionsfaktor größer als 1 ist. Dagegen kommt es zu einem exponentiellen Abklingen, wenn dieser Faktor kleiner als 1 ist.
Daraus ergibt sich eine interessante Schlussfolgerung: Um einen massiven Ausbruch einer Epidemie zu verhindern, muss man Ansteckungen nicht etwa perfekt vermeiden. Es genügt, den Reproduktionsfaktor etwas unter 1 zu drücken – was zu einem negativen Wachstumskoeffizienten führt.
Sind die ergriffenen Anstrengungen aber etwas zu schwach, sodass der Reproduktionsfaktor immer noch über 1 liegt, erhält man weiter ein exponentielles Wachstum – nur eben ein verlangsamtes. Damit darf man sich nicht begnügen, wenn man die Ansteckung eines großen Teils der Bevölkerung vermeiden will. Dies gilt beispielsweise in der 2019 begonnenen Coronaviren-Pandemie: Nur die Zahl der Intensivpflegeplätze in den Krankenhäusern zu erhöhen, könnte das Problem nicht lösen, da die Last bei exponentiellem Wachstum jede Kapazitätsgrenze früher oder später übersteigen würde. Eine solche Strategie wäre genauso erfolgversprechend, wie auf offenem Meer vor einem Hai durch schnelles Schwimmen zu flüchten: Der Hai ist immer schneller als Sie.
Natürlich ist auch ohne aktive Gegenmaßnahmen kein grenzenloses Wachstum einer Epidemie möglich: Mehr als 100 % einer Bevölkerung können ja nie infiziert werden. Bereits etwas bevor dies erreicht wird, nehmen der Reproduktionsfaktor und die Rate der neuen Ansteckungen deutlich ab, weil die Infizierten von immer weniger noch nicht infizierten Menschen umgeben sind, die man noch anstecken könnte. Ein konstanter Reproduktionsfaktor und ein konstanter Wachstumskoeffizient – die Merkmale exponentiellen Wachstums – sind eben nur möglich, solange der Großteil der Bevölkerung noch nicht infiziert wurde. Aber am Ende erwischt es dann eben doch die meisten – ohne Grund klingt eine Epidemie nicht ab, wie auch Donald Trump im Frühjahr 2020 schmerzlich (vor allem für andere) lernen musste.
Auch auf andere Weisen kann der Reproduktionsfaktor reduziert werden – einige Beispiele:
- Man kann durch reduzierte soziale Kontakte ("social distancing") die Wahrscheinlichkeit von Übertragungen reduzieren.
- Wenn es eine massenhaft anwendbare Impfung gibt, kann man u. U. so viele Menschen rechtzeitig immunisieren, dass der Reproduktionsfaktor kleiner 1 wird, lange bevor die Krankheit einen wesentlichen Teil der Bevölkerung erfasst hat.
- Wenn sich die Wetterverhältnisse so ändern, dass dies die Ansteckungen wesentlich reduziert, führt dies manchmal dazu, dass eine Krankheitswelle von selbst wieder abklingt.
Im Zusammenhang mit der Corona-Pandemie war besonders anfangs häufig zu beobachten, dass ein Verständnis der wesentlichen Aspekte dieser Krise am fehlenden Verständnis für exponentielles Wachstum scheitert. Auch sonst vernünftige Menschen konnten es sich einfach nicht vorstellen, dass die Zunahme von Infektionen auf damals noch geringem Niveau rasch zu einem wesentlichen Problem führen. Das dürfte einer der Gründe dafür sein, dass viele Menschen irreführenden Fehlinterpretationen aufsaßen. Freilich gab es noch etliche andere Gründe, die ich in meinem Artikel über die Aufdeckung von Irrtümern analysiert habe.
Im Einzelnen sind die Verhältnisse bei Epidemien aus diversen Gründen natürlich um einiges komplizierter als z. B. beim Wachstum von Bakterien in einer Nährlösung. Beispielsweise kann die Ansteckungswahrscheinlichkeit innerhalb einer Familie oder einer Arbeitsgruppe recht hoch sein, über die Grenzen solcher Gruppen hinweg dagegen geringer. Außerdem lässt sich oft schwer rechnen, da z. B. die Anzahl der bereits Infizierten nicht so leicht ermittelbar ist. Der möglichst intelligente Umgang mit diesen und etlichen weiteren Problemen gehört zur zentralen Aufgabe der Epidemiologie.
Virale Verbreitung von Informationen
Informationen können ähnlich wie Krankheitserreger von Mensch zu Mensch übertragen werden. So etwas kann man oft auch mit statistischen Modellen beschreiben. Ein Reproduktionsfaktor kann auch hier definiert werden – als die durchschnittliche Anzahl von Menschen, die von einem informiert werden, der die Information bekommen hat. Wiederum kommt es zu einer exponentiellen Verbreitung der Information, wenn dieser Reproduktionsfaktor größer als 1 wird, oder eben zu einem exponentiellen Auslaufen (Abklingen), wenn er kleiner als 1 ist.
Der Reproduktionsfaktor hängt hier davon ab, wie spannend eine Nachricht ist, bzw. genauer gesagt wie sehr sie die Empfänger dazu anregt, sie weiter zu verbreiten. Natürlich spielt es auch eine Rolle, wie einfach die Weiterverbreitung für die Menschen ist. Soziale Medien erlauben eine besonders einfache und schnelle Weiterverbreitung – oft mit gerade mal ein oder zwei Mausklicks.
Nur der geringste Teil der Nachrichten erreicht einen Reproduktionsfaktor oberhalb von 1; in solchen Fällen spricht man von "viralen" Nachrichten bzw. von einer viralen Verbreitung derselben. Die Zahl der erreichten Menschen wächst in etwa exponentiell an – zunächst langsam, dann immer schneller. Eine solche Informationswelle ebbt meist erst ab, nachdem sie sehr viele Menschen erreicht hat und ihr allmählich der Restbestand an noch nicht erreichten Menschen ausgeht.
Interessant ist die Einsicht, dass man die weite Verbreitung einer nicht viralen Nachricht – etwa mit einem Reproduktionsfaktor von 0,8 – kaum erzwingen kann, etwa indem man sie an möglichst viele Menschen schickt. Wenn man nicht gerade jemand wie Donald Trump ist, den Milliarden mit Bewunderung oder Grausen beobachten, erreicht man ohne Viralität seiner Nachricht niemals annähernd so viele Menschen wie bei viraler Verbreitung.
Leider gelingt eine virale Verbreitung nur sehr selten mit hochwertigen Nachrichten, sondern eher für solche, die mit mehr oder weniger unseriösen Methoden irgendwelche Emotionen geschickt ausnutzen. Beispielsweise gelingt das gelegentlich mit Nachrichten, die den Eindruck erwecken, man müsse sie unbedingt weiterverbreiten, um eine finstere Verschwörung zu bekämpfen. Dagegen hat ein Text wie dieser, der intensives Nachdenken erfordert (für viele Menschen viel zu anstrengend!), kaum eine Chance dafür. Wenn Sie das trotzdem fördern möchten, finden Sie ganz unten auf der Seite geeignete Schaltflächen für die Verbreitung über soziale Medien!
Zinsen auf angelegtes Kapital
Wenn Sie jemandem Geld leihen, werden Sie dafür in der Regel einen Zins als Gegenleistung erhalten. Sie können Ihr Kapital auf diese Weise also allmählich vermehren. Wenn der Zinssatz konstant ist und Sie die erhaltenen Zinsen jeweils konsumieren, wächst das Kapital nur linear an, d. h. jedes Jahr um den gleichen Betrag. Wenn Sie jedoch die Zinsen stets dem Kapital hinzufügen, erhalten Sie zukünftig auch auf diese wiederum Zinsen (sogenannte Zinseszinsen), und es kommt zu einem exponentiellen Wachstum des Kapitals. Nur geht das heutzutage leider nicht mehr sehr schnell, da die Zinssätze so niedrig geworden sind – außer Sie leihen das Geld jemandem, der einen hohen Zinssatz akzeptieren muss, weil Ihr Ausfallrisiko so hoch ist.
Wenn man nicht nur den nominalen Geldbetrag, sondern auch die Geldentwertung (Inflation) berücksichtigen möchte, kommt man manchmal effektiv sogar auf negative Erträge, jedenfalls mit sicheren Anlagen. In diesem Sinne schmilzt das Vermögen dann allmählich ab – bei konstanter Verlustrate auf exponentielle Weise.
Komplizierter als in vielen anderen Wachstumsphänomenen ist beim Geld der Umstand, dass Zinsen nicht kontinuierlich anfallen, sondern in regelmäßigen Abständen gezahlt werden. Deswegen steigt das Kapital eigentlich stufenweise und nicht wirklich exponentiell – was aber für die langfristige Betrachtung keine wesentliche Rolle spielt.
Wirtschaftswachstum
Viele Ökonomen gehen davon aus, dass ein stetiges Wirtschaftswachstum, idealerweise von mehreren Prozent pro Jahr, unabdingbar sei – nicht nur für die weitere Vermehrung des Wohlstands bzw. die Überwindung von Armut, sondern als Grundvoraussetzung für die Stabilität des gesamten Wirtschaftssystems und unserer Gesellschaft.
Ein konstantes Wirtschaftswachstum (d. h. eine konstante Wachstumsrate) entspräche einem exponentiellen Wachstum des Bruttosozialproducts. Mit dessen Steigerung geht üblicherweise der vermehrte Verbrauch von Ressourcen einher, ebenso die vermehrte Produktion von Abfällen, Schadstoffen u. ä., und insbesondere auch des klimaschädlichen Kohlendioxids. Offensichtlich würde anhaltendes exponentielles Wachstum früher oder später in eine Katastrophe führen und nicht etwa zu Stabilität und dauerhaftem Wohlstand. Wir stoßen bereits vielerorts an die Grenzen des Wachstums, nachdem weite Teile unserer Wirtschaft auf Raubbau basieren und nicht etwa auf Nachhaltigkeit.
Im Prinzip könnte dieses Dilemma aufgelöst werden, wenn Wohlstand auf der einen Seite und Ressourcenverbrauch und Umweltzerstörung auf der anderen Seite voneinander entkoppelt werden könnte – etwa durch verbesserte Energieeffizienz. Diese Entkopplung ist bislang ein Stück weit gelungen, jedoch werden Zugewinne an Effizienz meist am Ende durch zusätzlichen Verbrauch wieder zunichte gemacht, was die Ressourcen- und Umweltbelastung betrifft (→ Rebound-Effekt). Somit bleibt die Herausforderung bestehen, entweder die genannte Entkopplung entscheidend zu verstärken und so wirklich eine Begrenzung von Ressourcenverbrauch und Umweltbelastung zu erreichen, oder aber unser Wirtschaftssystem auf einen Zustand ohne dauerndes Wachstum umzustellen. Wenn das nicht gelingt, wird das Wachstum irgendwann ungeplant durch katastrophale Vorgänge beendet werden.
Atombombe und Kernreaktor
In einer Atombombe (Nuklearwaffe) wird eine nukleare Kettenreaktion ausgenutzt, die über einen Zeitraum von rund einiger Mikrosekunde (1 μs) zu einem massiven exponentiellen Anstieg der erzeugten Strahlung und freigesetzten Energie führt. Dies ist dadurch möglich, dass die Kernspaltung bestimmter Sorten von Atomen (Nuklide) Neutronen freisetzt, die wiederum die Spaltung weiterer Atome, auf die sie treffen, auslösen können. In dieser Situation ist das Wachstum der Neutronenstrahlung und der Energiefreisetzung etwa exponentiell, solange noch genügend spaltbare Atome verfügbar bleiben. Die Kettenreaktion endet allerdings deutlich bevor alle spaltbaren Atome gespalten sind, da die Explosion das Material auseinander treibt und damit die Wahrscheinlichkeit reduziert, dass spaltbare Atome noch von Neutronen getroffen werden. Jedoch genügt die Spaltung von ein paar Prozent des Materials für eine Explosion mit katastrophalen Folgen. Zum Glück ist es technisch nicht ganz einfach, die Umsetzung von einigen Prozent des spaltbaren Materials zu erzielen.
Eine Wasserstoffbombe basiert auf einer Kettenreaktionen mit Kernfusion statt mit Kernspaltung, wobei diese Reaktion aber von einer Kernspaltungsbombe initiiert wird. Qualitativ gelten die obigen Überlegungen hier ebenfalls, nur dass nochmals viel mehr Energie freigesetzt werden kann.
Ein Kernreaktor für die Gewinnung von Kernenergie wird üblicherweise über lange Zeit mit einer ziemlich genau konstanten Rate der Kettenreaktion betrieben, um eine konstante Wärmeleistung zu erhalten. Dies bedeutet, dass der Wachstumskoeffizient sehr nahe bei Null liegen muss, sodass es weder ein Wachstum noch einen Abfall der Leistung gibt. Dies ist nur möglich durch eine schnelle aktive Regelung, die auf Abweichungen von der gewünschten Leistung sehr schnell reagiert, indem sie z. B. Regelstäbe mehr oder weniger in den Reaktor eintaucht.
Übrigens wäre diese Regelung der Leistung eines Kernreaktors angesichts der schnellen nuklearen Prozesse extrem schwierig, wenn nicht ein Teil der Neutronen von Spaltprodukten (also radioaktivem Abfall in den Brennstäben) mit einer gewissen Verzögerung freigesetzt würde, die das System wesentlich träger und damit handhabbarer macht. (Das einfache Modell mit exponentiellem Wachstum entspricht also nicht ganz der etwas komplexeren Realität.) Auch andere Umstände, etwa das Vorhandensein bestimmter Transurane oder Spaltprodukte, können sich sehr nachteilig auf die Regelbarkeit eines Reaktors auswirken. Deswegen sind je nach Reaktortyp bestimmte Betriebszustände, in denen die Regelung der Kritikalität nicht mehr sicher gewährleistet wäre, streng verboten. Der Super-GAU von Tschernobyl wurde übrigens dadurch verursacht, dass ein solches Verbot im Rahmen von Experimenten (ironischerweise mit dem Ziel der Verbesserung der Sicherheit!) missachtet wurde. Es kam dabei zu einem unkontrollierten rapiden Anstieg der Reaktorleistung, der nicht mehr schnell genug gestoppt werden konnte, um eine Zerstörung von Reaktor und Gebäude durch diesen Kritikalitätsunfall zu vermeiden.
Laser
Ein Laser enthält eine Anordnung optischer Komponenten (einen Laserresonator), zwischen denen Licht ständig hin- und her laufen kann. Außerdem enthält diese Anordnung z. B. einen Laserkristall, der bei genügend starker Energiezufuhr (durch "optisches Pumpen") durchlaufendes Licht verstärken kann.
Wenn diese Verstärkung plötzlich eingeschaltet wird, während sich noch fast kein Licht im Resonator befindet, wird dieses Licht bei jedem Umlauf in seiner Leistung um z. B. einige Prozent verstärkt. Dies führt zu einem exponentiellen Wachstum, welches im Laufe einiger hundert oder einiger tausend Resonatorumläufe zu einer sehr hohen Leistung führen kann. Das Ansteigen der Leistung des Lasers wird irgendwann aber dadurch gestoppt, dass die im Laserkristall gespeicherte Energie (die Grundlage für die Verstärkung!) erschöpft wird; die Lichtleistung sinkt dann wieder rapide ab. Somit erhält man einen u. U. sehr intensiven Laserpuls (Lichtblitz), der in kürzester Zeit einen großen Teil der Energie transportiert, die vorher im Laserkristall gespeichert war. Der Laserkristall dient also im Grunde als eine Art von Energiespeicher, der innerhalb vergleichsweise langer Zeit (z. B. 0,0001 Sekunden) aufgeladen wird und diese Energie innerhalb von viel kürzerer Zeit wieder abgeben kann.
Aufgrund der hohen Geschwindigkeit des Lichts dauert ein Umlauf im Resonator nur z. B. eine Nanosekunde (eine Milliardstel Sekunde) oder bei einem kompakten Aufbau sogar noch deutlich weniger, und entsprechend kurz wird die Dauer des erzeugten Lichtblitzes: häufig nur einige Nanosekunden. In dieser Zeit ist das Licht aber extrem intensiv – oft genügend intensiv, um getroffenes Material unmittelbar zu verdampfen. Solche Laserpulse werden heute breit angewandt, insbesondere für die Lasermaterialbearbeitung. Allerdings verwendet man zunehmend auch sogenannte ultrakurze Laserpulse mit noch viel kürzeren Dauern, die ganz anders erzeugt werden (also nicht mit dem oben beschriebenen Prinzip). Eine exponentielle Verstärkung wird oft anderweitig ausgenutzt, um diese anfänglich recht energiearmen Lichtpulse ordentlich aufzumöbeln.
Als Laserphysiker ist der Autor dieses Artikels mit dem Phänomen des exponentiellen Wachstums bestens vertraut. Deswegen hat er auch die Zusammenhänge bei der Corona-Pandemie rasch erfasst und in 2020 einen Artikel mit dem Titel "Laser physics helps to understand the corona virus crisis" verfasst, der auf interessante Parallelen zwischen Pandemie und Vorgängen in Lasern hinwies.
Mechanische und andere Schwingungen; Anschwingen von Oszillatoren
Mechanische Schwingungen – etwa einer Gitarrensaite – klingen häufig exponentiell ab, wenn keine Energie mehr zugeführt wird. Das hängt damit zusammen, dass der Energieverlust pro Schwingungsperiode meist in guter Näherung proportional zur noch vorhandenen Energie der Schwingung ist. Ähnliches gilt auch für viele andere Arten gedämpfter Schwingungen, etwa von elektronischen Schwingkreisen.
Schwingungen können in manchen Situationen auch exponentiell anwachsen. So mancher Oszillator (Schwingungserzeuger) enthält einen Mechanismus, der einem schwingungsfähigen System bei der jeder Schwingungsperiode Energie zuführt, und zwar einen Betrag, der anfangs (d. h. kurz nach dem Einschalten) proportional zur bereits vorhandenen Schwingungsenergie ist. Wie Sie nun wissen, führt genau das zum exponentiellen Wachstum. Die genannte Proportionalität hört natürlich irgendwann auf, wenn die Schwingung zu stark wird; die verfügbare Leistung als Voraussetzung für die Verstärkung ist ja immer begrenzt. Die Schwingungsenergie spielt sich dann auf ein bestimmtes Niveau ein.
Theoretisch könnte man meinen, dass ein solcher Oszillator nicht von selbst anschwingen wird, weil die Schwingungsenergie anfangs ja null ist und dann der genannte Mechanismus auch keine Energie zuführen kann. Jedoch genügt in Wirklichkeit schon ein ganz winziges Quäntchen von Energie z. B. durch feinste Erschütterungen oder die thermische Bewegung. Durch das exponentielle Wachstum dauert es meist nicht allzu lange, bis eine starke Schwingung entsteht.
Ein Laser (siehe oben) ist eigentlich auch ein Beispiel für so einen Oszillator – nur eben nicht mit einer mechanischen Oszillation, sondern einer des elektromagnetischen Felds.

Wenn Ihnen diese Website gefällt, teilen Sie das doch auch Ihren Freunden und Kollegen mit – z. B. über Social Media durch einen Klick hier:
Diese Sharing-Buttons sind datenschutzfreundlich eingerichtet!