Lexikon > Buchstabe L > Leistungsfaktor

Leistungsfaktor

Bei Wechselstrom ist die effektiv übertragene Leistung (Wirkleistung) häufig geringer als die Scheinleistung, die man durch Multiplizieren der Effektivwerte von Spannung und Stromstärke erhält. (Dieses Phänomen wird im Artikel über Blindstrom erklärt.) Ein gebräuchliches Maß für dieses Phänomen ist der Wirkleistungsfaktor (oder kürzer Wirkfaktor), definiert als die Wirkleistung dividiert durch die Scheinleistung; er wird oft mit dem Formelbuchstaben <$\lambda$> bezeichnet und liegt stets zwischen 0 und 1. Im Idealfall mit Leistungsfaktor 1 gibt es keine Blindleistung, also keine zusätzliche Belastung der Leitungen durch einen Strom, der keine Wirkleistung überträgt.

Gründe für einen verminderten Leistungsfaktor

Phasenverschiebung zwischen Strom und Spannung

In der Praxis kommt es häufig vor, dass die Verläufe von Stromstärke und Spannung zwar beide sinusförmig sind, aber nicht die gleiche Phase haben, also zeitlich gegeneinander mehr oder weniger verschoben sind. Im Falle induktiver Verbraucher hinkt der Verlauf der Stromstärke dient der Spannung nach, während bei Verbrauchern mit kapazitiver Charakteristik die Stromstärke der Spannung vorauseilt.

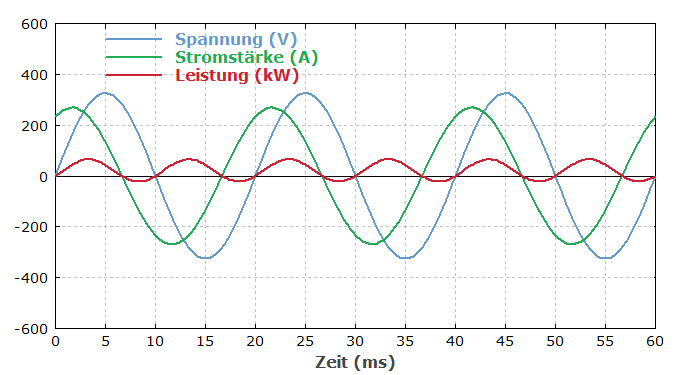
Die Stärke der Phasenverschiebung wird mit dem Phasenwinkel <$\varphi$> quantifiziert. In dieser Situation ist der Leistungsfaktor der Betrag des Kosinus des Phasenwinkels: <$\lambda = |\cos \varphi |$> (wobei dieser Kosinus normalerweise positiv ist). Für <$\cos \varphi$> gibt es auch die Bezeichnung Verschiebungsfaktor.

Im Extremfall ist der Phasenwinkel 90°. In diesem Falle (mit <$\lambda = |\cos \varphi | = 0$>) schwingt die übertragene Momentanleistung sinusförmig um den Mittelwert null (mit doppelter Netzfrequenz), und die Wirkleistung ist null. Die Energie pendelt dann nur zwischen Stromquelle und Verbraucher; im zeitlichen Durchschnitt wird keine Energie zum "Verbraucher" übertragen.

Nicht sinusförmiger Stromverlauf, Oberwellen

Ebenfalls kommt es häufig vor, dass der Verlauf der Stromstärke nicht sinusförmig ist. Dies ist beispielsweise der Fall bei Betrieb eines Gleichrichters; hier verschwindet die Stromstärke völlig zu Zeiten, in denen die Spannung betragsmäßig nicht hoch genug ist. Viele (vor allem kleinere) Schaltnetzteile enthalten einen einfachen Gleichrichter, der dieses Phänomen aufweist. Ein anderes Beispiel sind Dimmer mit Phasenanschnittsteuerung, wo die Stromstärke am Anfang einer Schwingungsperiode der Spannung zunächst null bleibt und dann plötzlich stark ansteigt. Hier hat man sowohl eine Phasenverschiebung als auch Oberwellen (siehe unten). Diesen Fall zeigt die folgende Abbildung:

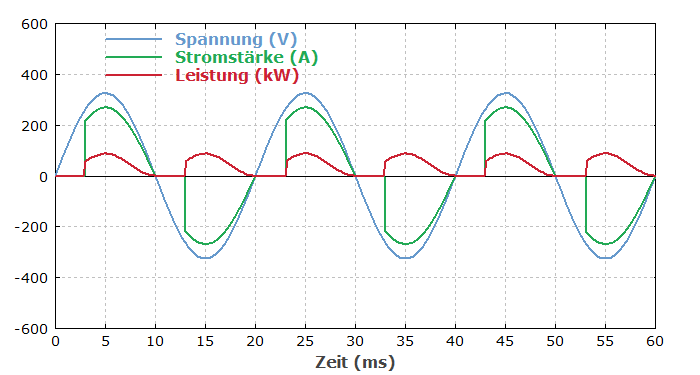
In diesem Falle nicht sinusförmig verlaufender Stromstärke ist die obige Formel <$\lambda = \cos \varphi$> nicht anwendbar; es ist nicht einmal offensichtlich, wie der Phasenwinkel dann überhaupt bestimmt werden sollte. Man kann den Leistungsfaktor dann also nicht einfach mit dem Wirkfaktor <$\cos \varphi$> (oder dessen Betrag) identifizieren. Stattdessen kann eine aufwändigere mathematische Prozedur verwendet werden. Wenn immerhin die Spannung sinusförmig verläuft (wie sie es normalerweise sollte), ist das Verfahren wie folgt:

• Man zerlegt den Verlauf der Stromstärke mittels Fourier-Analyse in ihre Frequenzanteile. Wir nehmen hier an, dass der Verlauf der Stromstärke periodisch ist, d. h. in jedem Schwingungszyklus der Spannung gleich. Dann sind die Frequenzen ganzzahlige Vielfache der Netzfrequenz: Man hat eine Kombination der Grundschwingung (mit der Netzfrequenz) und sogenannte Oberwellen mit höheren Frequenzen.
• Für die Grundschwingung kann man den Phasenwinkel <$\varphi$> bestimmen, und ihr Beitrag zur Wirkleistung ist <$U I_1 \cos \varphi$>, wobei <$U$> der Effektivwert der Spannung und <$I_1$> derjenige der Grundschwingung der Stromstärke ist.
• Die Oberwellen tragen zur Wirkleistung nichts bei.
• Der Leistungsfaktor ist also <$\lambda = (I_1 / I) \cos \varphi$>, wobei <$I$> der Effektivwert der Stromstärke (mit allen Frequenzanteilen) ist.

Gedanklich wesentlich einfacher ist eine numerische Berechnung, die einfach auf einer zeitlichen Integration der Momentanleistung über eine Schwingung basiert. Dieses Verfahren verwendet man beispielsweise in digitalen Leistungsfaktor-Messgeräten. Auch eine analoge Ermittlung des Leistungsfaktors basierend auf diesem Prinzip ist möglich.

Optimierung des Leistungsfaktors (Leistungsfaktorkorrektur)

Für die Übertragung hoher elektrischer Leistungen ist es wünschenswert, dass der Leistungsfaktor hoch ist (z. B. über 0,9). So wird vermieden, dass zusätzliche Energieverluste in der Leitung durch den Blindstrom-Anteil entstehen. Deswegen verlangen Energieversorger bei Großkunden einen ausreichend hohen Leistungsfaktor (ggf. erzielbar durch Einsatz von Blindleistungskompensation) oder verlangen für den Blindstromanteil ein zusätzliches Entgelt. Für kleine Verbraucher wie z. B. Haushaltslampen dagegen ist der Leistungsfaktor ziemlich belanglos; der Aufwand für eine detaillierte Optimierung würde sich nicht lohnen.

Technisch erfolgt die Optimierung des Leistungsfaktors häufig, indem man induktive oder kapazitive Elemente zugeschaltet, um den Phasenwinkel in der Leitung zu verkleinern. Dies funktioniert freilich nur dann, wenn der Phasenwinkel das eigentliche Problem ist.

Wenn dagegen Oberwellen auftreten, ist ein anderer Ansatz nötig. Eine relativ simple Möglichkeit ist der Einsatz passiver Oberschwingungsfilters – in der Regel drosseln mit großer Induktivität. Daneben gibt es auch aktive Oberschwingungsfilter, die als Zusatz zu Gleichrichtern einsetzbar sind. Hier realisiert man zunächst einen Aufwärtswandler, der so betrieben wird, dass die Stromstärke jeweils proportional zur momentanen Spannung ist. Solche Einrichtungen werden auch als Leistungsfaktorkorrekturfilter bezeichnet.

Siehe auch: Wechselstrom, Blindstrom, Scheinleistung, Blindleistungskompensation, Effektivwert von Spannung und Stromstärke