Lexikon > Buchstabe V > Verzerrungsblindleistung

Verzerrungsblindleistung

Wenn von Blindleistungen z. B. in Stromnetzen die Rede ist, dann meistens solche, die aus einer Phasenverschiebung zwischen elektrischer Stromstärke und elektrischer Spannung resultieren; dies ist die sogenannte Verschiebungsblindleistung. Jedoch entsteht eine Blindstromproblematik teilweise auch im Zusammenhang mit einem nicht sinusförmigen Verlauf der Stromstärke, wie er von manchen nichtlinearen Lasten verursacht wird; dieses Phänomen wird hier behandelt, und zwar besonders im Zusammenhang mit Stromleitungen und Stromnetzen. Man nennt es Verzerrungsblindleistung oder auch Oberschwingungsblindleistung. Es kommt sowohl bei Einphasen-Wechselstrom als auch bei Drehstrom vor, wobei es im letzteren Fall noch zusätzliche Konsequenzen haben kann.

Auswirkungen nicht sinusförmiger Stromverläufe

Zunächst einmal ist es möglich (und häufig hilfreich), jeden nicht sinusförmigen Stromverlaufs mithilfe einer sogenannten Fourier-Analyse in verschiedene Frequenzkomponenten aufzuteilen. Im Folgenden nehmen wir an, dass der Stromverlaufs periodisch ist, d. h. dass er während jeder Schwingungsperiode gleich verläuft. In diesem Fall gibt es nur Frequenzkomponenten, deren Frequenzen ganzzahlige Vielfache der Netzfrequenz (z. B. 50 Hz) sind. Die Komponente mit der Netzfrequenz wird hierbei als die Grundschwingung oder Grundwelle bezeichnet; die höheren Komponenten sind Oberwellen oder Harmonische.

Im einfachen Fall eines rein sinusförmigen Stromverlaufs (auch wenn eine Phasenverschiebung auftritt) liefert die Fourier-Analyse nur die Grundschwingung; Oberschwingungen kommen dann nicht vor bzw. haben die Amplitude null. Sobald jedoch eine Abweichung vom sinusförmigen Stromverlauf entsteht, tauchen mehr oder weniger starke Oberwellen auf. Der Effektivwert der Stromstärke ist hierbei die Summe der Effektivwerte aller Frequenzkomponenten.

Im Folgenden nehmen wir stets an, dass der Spannungsverlauf stets sinusförmig bleibt – was realistisch ist, solange nur genügend schwache nicht sinusförmige Ströme fließen und die Netzimpedanz nicht allzu groß ist. In diesem Fall führt nur die Grundschwingung des Stroms zur Übertragung einer Wirkleistung, weil die Spannung nur die Grundschwingung hat und jede Kombination der Grundschwingung der Spannung mit einer Oberwelle des Stroms nichts beiträgt. Jede Oberwelle für sich betrachtet führt nämlich nur zu einem Pendeln der Energie zwischen Stromquelle und Last, wie man es auch von einfachen induktiven und kapazitiven Lasten kennt; ihre Momentanleistung oszilliert sinusförmig um den Mittelwert null. Deswegen spricht man hier von Blindstrom: Die Oberwellen können nicht zum Netto-Energietransport zur Last beitragen, tragen aber sehr wohl zur Strombelastung der Stromleitung bei. Auf diese Weise beeinträchtigen sie auch die Energieeffizienz des Stromversorgungssystems, indem sie Energieverluste in der Stromleitung und in anderen Betriebsmitteln vergrößern.

Verwirrend kann zunächst sein, dass das genannte Pendeln der Energie zwischen Stromquelle und Last häufig nicht erkennbar ist, wenn man den Stromverlauf ohne Fourier-Analyse betrachtet: Häufig wird die übertragene Momentanleistung zu keiner Zeit negativ. (Als Beispiele betrachte man die unten diskutierten Fälle von Gleichrichter und Phasenanschnittsteuerung.) Deswegen mag es zunächst auch überraschen, dass man hier von Blindleistung spricht. Die Betrachtung einzelner Oberwellen, für die das genannte Pendeln der Energie klar auftritt, mag nun künstlich-mathematisch erscheinen – zumindest in Fällen, in denen die Gesamtheit der Oberwellen dieses Phänomen nicht zeigt. Jedoch könnte man beispielsweise mit bestimmten Filtern alle Oberwellen außer einer unterdrücken und dann das genannte Pendeln tatsächlich nachweisen können. Insofern kann man den Oberwellen ohne weiteres eine physikalische Realität zuweisen, sie also nicht nur als eine mathematische Merkwürdigkeit ansehen.

Mit der genannten Methodik der Fourier-Analyse kann man die Übertragung von Leistungen und folgendermaßen analysieren:

• Wie gesagt tragen die Oberwellen nichts zur Wirkleistung bei. Die Wirkleistung <$P$> ergibt sich also als einfach als Produkt der Effektivwerte von Spannung und Strom-Grundwelle, multipliziert mit dem Faktor <$\cos \varphi_1$>, wobei <$\varphi_1$> der Phasenwinkel der Grundwelle des Stroms ist. (Die Fourier-Analyse liefert diesen Wert für jede Frequenzkomponente zusätzlich zu deren Amplitude.)
• Die Scheinleistung <$S$> ist ohnehin einfach zu berechnen als Produkt der Effektivwerte von Strom und Spannung.
• Der Leistungsfaktor <$\lambda$> ist das Verhältnis von Wirk- und Scheinleistung: <$\lambda = P / S$>.
• Die gesamte Blindleistung ergibt sich aus <$Q_{\rm tot}^2 = S^2 - P^2$>. Sie kann weiter unterschieden werden in die Verschiebungsblindleistung <$Q$> und die Verzerrungsblindleistung <$D$>, wobei gilt <$Q_{\rm tot}^2 = Q^2 + D^2$>.
• Somit gilt außerdem auch <$S^2 = P^2 + Q^2 + D^2$>.

Prinzipiell sind die folgenden Arten von Auswirkungen einer Verzerrung des Stromverlaufs möglich:

• Der verminderte Leistungsfaktor bedeutet, dass die übertragene Wirkleistung im Verhältnis zur Belastung der Leitung reduziert ist. Entsprechend können die Energieverluste in der Leitung und in anderen Betriebsmitteln ansteigen, je nach deren Widerstand.
• Diejenigen Oberwellen, deren Ordnungszahl durch drei teilbar ist (vor allem die mit der dreifachen Netzfrequenz), tragen in einem Drehstromsystem zur Belastung des Neutralleiters bei, auch wenn keine Schieflast auftritt. Die Beiträge solcher Oberwellen zum Strom im Neutralleiter gleichen sich nämlich anders als die der Grundwelle nicht gegenseitig auf; sie haben nämlich alle die gleiche Phasenlage.
• Die Oberwellen können auch andere Auswirkungen haben, beispielsweise die Funktion anderer Betriebsmittel des Netzes oder anderer angeschlossener Verbraucher stören. Wie sehr dies der Fall ist, kommt allerdings nicht nur auf die Stärke der Oberwellen an, sondern auch auf die Beschaffenheit des Netzes (vor allem auf die Netzimpedanz bei den relevanten Frequenzen) und der Sensitivität der anderen Verbraucher.

Ursachen von Verzerrungen des Stromverlaufs

Zwei typische Beispiele für Lasten, die Verzerrungen des zeitlichen Stromverlaufs verursachen, werden im Folgenden erklärt.

Gleichrichter

Gleichrichter, vor allem einfache Brückengleichrichter in Verbindung mit einem Kondensator, sind Lasten mit erheblichen Nichtlinearitäten. Hier kann dem Netz nämlich nur zu solchen Zeiten Strom entnommen werden, in denen der Momentanwert der Spannung oberhalb der Kondensatorspannung liegt, während die Zuleitung zu anderen Zeiten praktisch stromlos bleibt.

Wir betrachten im Folgenden einen typischen Beispielfall:

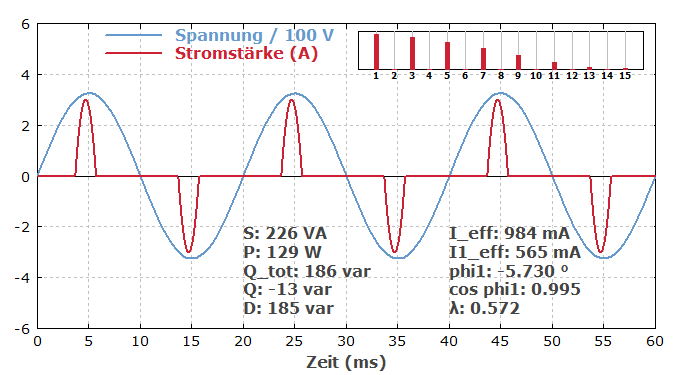
Abbildung 1 zeigt die Verläufe von Spannung und Strom, und sie zeigt alle essenziellen Parameter:

• Der Effektivwert des Stroms liegt hier weit unter dessen Spitzenwert, weil der Strom immer nur in ziemlich kurzen Zeitintervallen fließt.
• Der Leistungsfaktor ist mit 0,572 ziemlich gering. Dies drückt aus, dass die übertragene Wirkleistung im Verhältnis zur Belastung des Stromnetzes ziemlich klein ist.
• Es gibt nur eine minimale Verschiebungsblindleistung kapazitiver Art. Diese rührt daher, dass das Maximum des Stroms ein wenig vor dem Spannungsmaximum erreicht wird, weil die Spannung am Glättungskondensator in dieser Zeit etwas ansteigt.
• Die Verzerrungsblindleistung dagegen ist erheblich – betragsmäßig nicht viel kleiner als die Scheinleistung. Sie ist die wichtigste Ursache für den verminderten Leistungsfaktor.
• Der Effektivwert der Grundschwingung des Stroms (565 mA) ist weit kleiner als der gesamte Effektivwert (984 mW); die fehlenden 419 mA gehören zu den Oberwellen, die zur Wirkleistung nichts beitragen. Die Verteilung der Effektivwerte auf die Oberwellen wird in dem kleinen Diagramm oben rechts gezeigt; es tauchen hier nur ungeradzahlige Oberwellen auf. Je schmaler die Strom-Peaks im Zeitverlauf sind, desto stärker ausgeprägt sind diese Oberwellen. Manchmal vermindert man die Intensität der höheren Oberwellen, indem man mithilfe einer zusätzlichen Drosselspule den zeitlichen Verlauf des Stroms streckt. Dies verbessert dann auch den Leistungsfaktor.

Dimmer und Drehzahlregler

Dimmer und Drehzahlregler für Elektromotoren, die mit einer Phasenanschnittsteuerung arbeiten, verursachen einen Stromverlauf mit steilen Schaltflanken (vor allem im mittleren Leistungsbereich).

Wir betrachten wieder ein Beispiel; ein Dimmer ist hier auf etwas mehr als die Hälfte der vollen Leistung eingestellt und speist eine rein ohmsche Last:

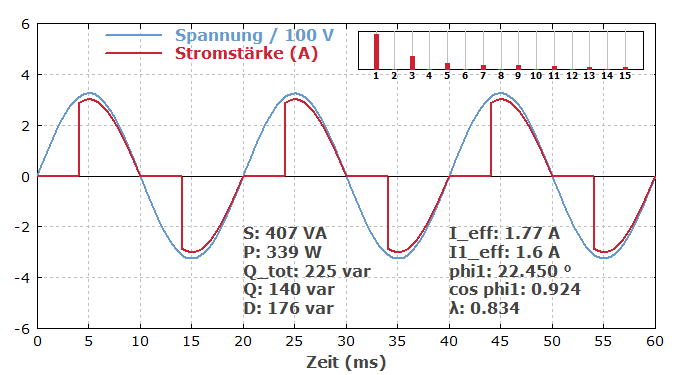
Anmerkungen zu den Parametern:

• Die Wirkleistung liegt wieder deutlich unterhalb der Scheinleistung, was auch der Leistungsfaktor von 0,834 ausdrückt.
• In diesem Fall gibt es eine erhebliche Verschiebungsblindleistung, da die Grundwelle des Stroms um 22,45° gegenüber der Spannung verzögert ist.
• Zusätzlich gibt es eine erhebliche Verzerrungsblindleistung, die durch die starke Abweichung von einem sinusförmigen Stromverlauf verursacht wird.
• Der Leistungsfaktor liegt deutlich unterhalb von <$\cos \varphi_1$>, dem Verschiebungsfaktor oder Wirkfaktor der Grundwelle, weil zusätzlich einiges an Blindleistung in den Oberwellen steckt, was den Leistungsfaktor weiter reduziert.

Transformatoren und Drosselspulen

Transformatoren und Drosselspulen weisen Nichtlinearitäten auf, wenn ihr Eisenkern in die Sättigung gerät – wenn also das Eisen schon voll magnetisiert ist und eine weitere Erhöhung der Stromstärke in den Wicklungen deswegen keine wesentliche Verstärkung des Magnetfeldes mehr bewirken kann. Normalerweise werden solche Betriebsmittel allerdings so bemessen, dass im Normalbetrieb keine magnetische Sättigung auftritt. Beim Betrieb mit Überspannung kann sich dies aber schnell ändern.

Kompensation oder Vermeidung von Verzerrungsblindleistungen

Während eine Verschiebungsblindleistung durch Zufügen eines Kondensator oder einer Drosselspule relativ einfach kompensiert werden kann, ist dies bei Verzerrungsblindleistungen wesentlich schwieriger. In der Regel versucht man dieses Phänomen eher von vornherein zu vermeiden, beispielsweise indem man Gleichrichterschaltungen mit einer aufwendiger Technik einsetzt sowie Transformatoren und Drosselspulen so auslegt, dass sie zumindest im Bemessungsbetrieb keine nennenswerte magnetische Sättigung erreichen.

Bei kleinen Verbrauchern sind die Auswirkungen einer Verzerrung des Stromverlaufs oft so geringfügig, dass keine besonderen Maßnahmen dagegen notwendig oder angemessen sind. Andernfalls versucht man Oberwellen mit allzu hoher Ordnung zu unterdrücken, um Störungen zu vermeiden. Für Geräte ab 75 W Nennleistung gibt es z. B. gemäß der Norm IEC/EN61000 Vorschriften zur Begrenzung des Oberwellenspektrums.

Siehe auch: Blindstrom, Blindleistung